Oscillators and Waves

A professor of mine once said that everything in physics is a simple harmonic oscillator. Therefore it is necessary to get a handle on everything.

The Simple Harmonic Oscillator (SHO)

The differential equation for a simple harmonic oscillator in one dimension can be express with quaternion operators.

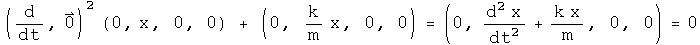
\(d by dt, 0\) squared acting on \(0, x, 0, 0\) + \(0, k x over m, 0, 0\) = \(0,x double dot + k x/m, 0, 0\) = 0

This equation can be solved directly.

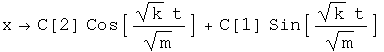
x = C\(2\) cosine \(the square root of k over m times t\) + C\(1\) sine \(the square root of k over m times t\)

Find the velocity by taking the derivative with respect to time.

x dot = the square root of k over m times C\(1\) cosine \(the square root of k over m times t\) - the square root of k over m times times C\(2\) sine \(the square root of k over m times t\))

The Damped Simple Harmonic Oscillator

Generate the differential equation for a damped simple harmonic oscillator as done above.

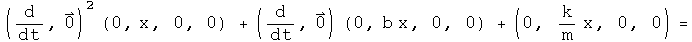
\(d by dt,0\) squared acting on \(0,x, 0, 0\) + \(d by dt,0\) acting on \(0, b x, 0, 0\) + \(0, k x over m,0,0\) =

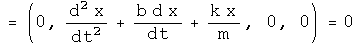
= \(0, x double dot + b x dot + k x over m, 0, 0\) = 0

Solve the equation.

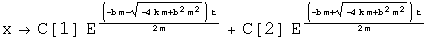
x = c1 times e to the - b - the square root of b squared - 4 k over m over 2 times t + c2 times e to the - b + the square root of b squared - 4 k over m over 2 times t

The Wave Equation

Consider a wave traveling along the x direction. The equation which governs its motion is given by

\(1/v d by dt,d by dx, 0, 0\) squared acting on \(0, 0, f\(t v + x\), 0) =

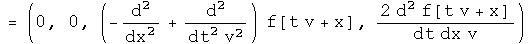
=\(0, 0, \(-d squared by d x squared +1/v squared d squared by d t squared \) f\(t v+x\), 2 d squared f\(t v + x\)/v dt dx)

The third term is the one dimensional wave equation. The forth term is the instantaneous power transmitted by the wave.

Implications

Using the appropriate combinations of quaternion operators, the classical simple harmonic oscillator and wave equation were written out and solved. The functional definition of classical physics employed here is that the time operator is decoupled from any space operator. There is no reason why a similar combination of operators cannot be used when time and space operators are not decoupled. In fact, the four Maxwell equations appear to be one nonhomogeneous quaternion wave equation, and the structure of the simple harmonic oscillator appears in the Klein-Gordon equation.