EM invariants

To derive the field equations of electromagnetism (EM), we need to find Lorentz invariants that use the electric (E) and magnetic (B) fields of EM that then get plugged into the Euler-Lagrange equation.

An invariant is something all observers can agree on. The Egyptians figure out one long ago:

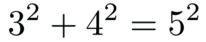
3 squared plus 4 squared equals 5 squared

This was the basis for surveying in the flood plains of the Nile. It remains true today. The 3D Egyptians know we could also include a third spacial dimension:

a squared plus b squared plus c squared equals R squared

Einstein showed that Egyptians in rockets could only agree on the interval between events.

d tau squared equals d t squared minus d R squared over the speed of light c squared

Accelerating or spinning is alright for observing events is you can figure out the right sort of functions to put into the interval.

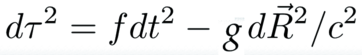
d tau squared equals the function f times d t squared minus the function g times d R squared over the speed of light c squared

Masters of general relativity can figure out the dynamic functions for f and g in only a few special cases because the math remains so difficult. The proposal described in this site, quaternion gravity, should make this issue tractable since then one has an algebra problem instead of ten nonlinear differential equations to solve. For the rest of the discussion of EM, it is assumed f and g are equal to one since it makes the math simple.

The first term of a quaternion product is a Lorentz invariant scalar. Couple the current with the potential by multiplying them together:

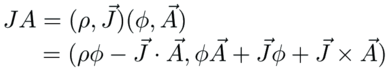
J times A equals rho, J times phi, A equals r phi minus J dot A, phi A plus J phi plus the cross product of J and A

The electric and magnetic fields can be written in terms of differential operators acting on a potential. Form the product:

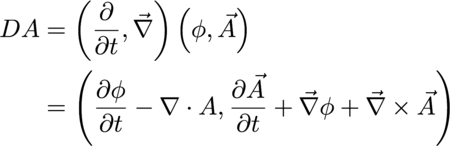
The differential times the potential A equals the time derivative, Del times phi A equals the time derivative of phi minus the divergence of A, the time derivative of A plus the gradient of phi plus the curl of A

The first term is a gauge term. EM has gauge symmetry. Set this to zero in a way that assures that no matter what gauge we pick - terms involving the time derivative of phi or divergence of A - the other terms are unchanged.

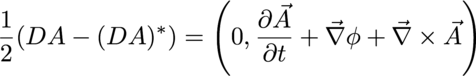
One half Del times A minus the conjugate of Del times A equals zero the time derivative of A plus the gradient of phi plus the curl of A

There are two times of 3-vectors. An axial vector will not change if the order of the product is reverse. A polar vector will flip signs by changing the order. That is a property of cross products and curls. Here are the two possibilities:

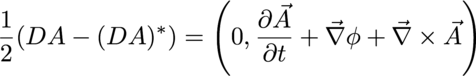
One half Del times A minus the conjugate of Del times A equals zero the time derivative of A plus the gradient of phi plus the curl of A

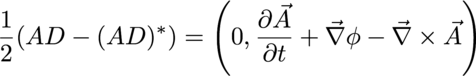
One half A times Del minus the conjugate of A times Del equals zero the time derivative of A plus the gradient of phi minus the curl of A

These should both be as "long" as each other, but will point in a different direction so long as the magnetic field B is not zero. Zero is an invariant, so take the difference of the norms of both of these, and that will always, necessarily, be equal to zero.

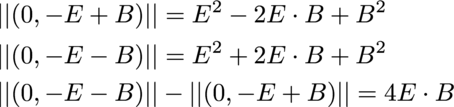
The norm of minus E plus B equals E squared minus 2 E dot B plus B squared. The norm of minus E minus B equals E squared plus 2 E dot B plus B squared. The second norm minus the first is 4 E dot B

The dot product of the electric and magnetic field will be used to derive the homogeneous Maxwell equations, the no monopoles and Faraday's law.

The product of the two ways to multiply a differential and a potential also form an invariant:

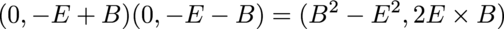
0, minus E plus B times 0, minus E minus B equals B squared minus E squared, 2 E cross B

This Lorentz invariant quantity will be used when deriving the Maxwell source equations, Gauss' and Ampere's laws.

Combine all these smaller observations into one expression:

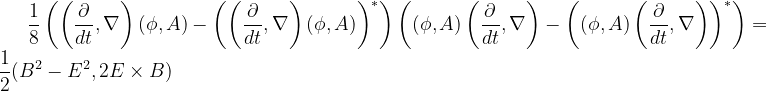
Is this "complicated look" necessary or does it reveal something? I vote for the latter. The 4-derivative of a 4-potential has the electric and magnetic fields without further adjustment, a remarkable thing. It also has a gauge field. It is my hope this is a great thing for particles with mass. For a theory of photons that have no rest mass, that field must be set to zero. That is accomplished with the subtractions. The Lorentz invariant is the difference of two squares of the magnetic and electric fields. That is achieved by swapping the order of the derivative and potential.

The other term is called Poynting's vector. It is the energy flux of the electromagnetic field. It is this vector that "gets work done". I confess to thinking worked was done by pushing electrons here and there. There are several videos on the web that will clarify how important the Poynting vector is to understanding work done by electromagnetism: Veritasium, 2021-11-19 and The Science Asylum, 2019-01-31. My new perspective is that work gets done in a particular direction, so that is where the Poynting vector comes into play. Note that because of resistence, in practice the electric and magnetic fields are not at 90-degree angles. No doubt there is an equation for that, but I do not know it yet.