Commutators and the Uncertainty Principle

Commutators and the uncertainty principle are central to quantum mechanics. Using quaternions in these roles has already been established by others (Horwitz and Biedenharn, Annals of Physics, 157:432, 1984). The first proof of the uncertainty principle I saw relied solely on the properties of complex numbers, not on physics! In this notebook I will repeat that analysis, showing how commutators and an uncertainty principle arise from the properties of quaternions (or their subfield the complex numbers).

Commutators

Any quaternion can be written in a polar form.

q = \(s, V\) = root q conjugated q times e to the \(s over root q conjugated times q times V over root V conjugate times V\)

This is identical to Euler's formula except that the imaginary unit vector i is replaced by the normalized 3-vector. The two are equivalent if j = k = 0. Any quaternion could be the limit of the sum of an infinite number of other quaternions expressed in a polar form. I hope to show that such a quaternion mathematically behaves like the wave function of quantum mechanics, even if the notation is different.

To simplify things, use a normalized quaternion, so that q q = 1. Collect the normalized 3-vector together with I = V/(V V)^.5.

The angle s/(q* q)^.5 is a real number. Any real number can be viewed as the product of two other real numbers. This seemingly irrelevant observation lends much of the flexibility seen in quantum mechanics :-) Here is the rewrite of q.

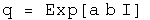
q = e to the \(a b I\)

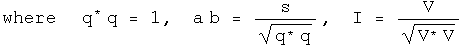
where q conjugate times q = 1, a b = s over root q conjugated times q, I = V over root V conjugated times V

The unit vector I could also be viewed as the product of two quaternions.For classical quantum mechanics, this additional complication is unnecessary. It may be required for relativistic quantum mechanics, so this should be kept in mind.

A point of clarification on notation:the same letter will be used 4 distinct ways.There are operators, A hat, which act on a quaternion wave function by multiplying by a quaternion, capital A. If the operator A hat is an observable, then it generates a real number, (a, 0), which commutes with all quaternions, whatever their form. There is also a variable with respect to a component of a quaternion, a_i, that can be used to form a differential operator.

Define a linear operator A hat that multiplies q by the quaternion A.

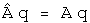
A hat acts on q = A times q

If the operator A hat is an observable, then the quaternion A is a real number, (a, 0). This will commute with any quaternion. This equation is functionally equivalent to an eigenvalue equation, with A hat as an eigenvector of q and (a, 0) as the eigenvalue. However, all of the components of this equation are quaternions, not separate structures such as an operator belonging to a group and a vector. This might make a subtle but significant difference for the mathematical structure of the theory, a point that will not be investigated here.

Define a linear operator B hat that multiplies q by the quaternion B. If B hat is an observable, then this operator can be defined in terms of the scalar variable a.

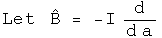
Let B hat = - I d by d a

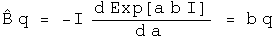
B hat acting on q = - I d e to the \(a b I\) over d a = b times q

Operators A and B are linear.

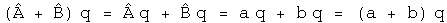
\(A hat + B hat\) acting on q = A hat acting on q + B hat acting on q = a times q + b times q = \(a + b\) times q

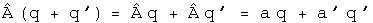
A hat acting on \(q + q prime\) = A hat acting on q + A hat acting on q prime = a times q + a prime times q prime

Calculate the commutator [A, B], which involves the scalar a and the derivative with respect to a.

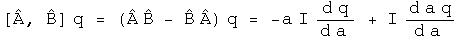
The commutator of A hat, B hat acting on q = \(A hat times B hat - B hat times A hat\) acting on q = -a I d q by d a + I d a q by d a

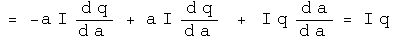
= -a I d q by d a + a I d q by d a + I q d a by d a = I q

The commutator acting on a quaternion is equivalent to multiplying that quaternion by the normalized 3-vector I.

The Uncertainty Principle

Use these operators to construct things that behave like averages (expectation values) and standard deviations.

The scalar a--generated by the observable operator A hat acting on the normalized q--can be calculated using the Euclidean product.

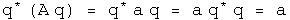
q conjugated \(A hat acting on q\) = q conjugated a q = a q conjugated q = a

It is hard to shuffle quaternions or their operators around. Real scalars commute with any quaternion and are their own conjugates. Operators that generate such scalars can move around. Look at ways to express the expectation value of A.

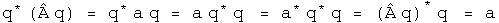
q conjugated \(A hat acting on q\) = q conjugated a q = a q conjugated q = A conjugated q conjugated q = \(A hat acting on q\) conjugated q = a

Define a new operator A' based on A whose expectation value is always zero.

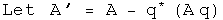
Let A prime = A hat - q conjugated \(A hat acting on q\)

q conjugated \(A prime q\) = q conjugated \(A - q conjugated \(A q\))q) = a - a = 0

Define the square of the operator in a way designed to link up with the standard deviation.

Let DA prime squared = q conjugated \(A prime acting twice on q\) - \(q conjugated \(A prime q\)) squared = q conjugated \(A prime acting twice on q\)

An identical set of tools can be defined for B.

In the section on bracket notation, the Schwarz inequality for quaternions was shown.

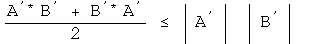
\(A prime conjugated times B prime + B prime conjugated times A prime\) over 2 is less than the absolute value of A prime times the absolute value of B prime

The Schwarz inequality applies to quaternions, not quaternion operators. If the operators A' and B' are surrounded on both sides by q and q*, then they will behave like scalars.

The left-hand side of the Schwarz inequality can be rearranged to form a commutator.

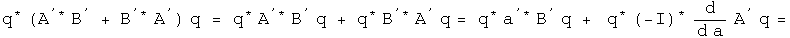
q conjugated \(A prime conjugated B prime + B prime conjugated A prime\) q = q A prime conjugated B prime q + q B prime conjugated A prime q = q conjugated A prime conjugated B prime q + q conjugated \(-I\)conjugated d by d a A prime q =

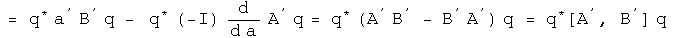
= q conjugated A prime B prime q - q conjugated \(-I\)d by d a A prime q = q conjugated\(A prime B prime - B prime A prime\)q = q conjugated times the conjugator of \(A prime, B prime\) q

The right-hand side of the Schwarz inequality can be rearranged to form the square of the standard deviation operators.

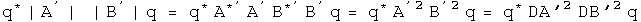
q conjugated times the absolute value of A prime times the absolute value of B prime times q = q conjugated A prime A primeB prime conjugated B prime q = q A prime squared B prime squared q = q conjugated DA prime squared DB prime squared q

Plug both of these back into the Schwarz inequality, stripping the primes and the q's which appear on both sides along the way.

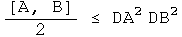
The commutator of A, B over 2 is less than the standard deviation squared of the operator A times the standard deviation squared of the operator B

This is the uncertainty principle for complementary observable operators.

Connections to Standard Notation

This quaternion exercise can be mapped to the standard notation used in physics

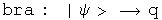
bra vector: |psi> maps to q

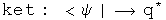
ket vector: <psi| maps to q conjugated

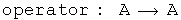
operator: A maps to A

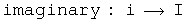
imaginary: i maps to 3-vector I

commutator: [A, B] maps to [A, B]

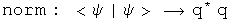
norm: <psi|psi> maps to q conjugated times q

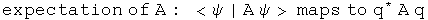
expectation of A: <psi|A psi> maps to q conjugated A q

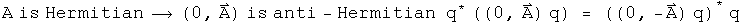
A is Hermitian maps to \(0, A\) is anti-Hermitian

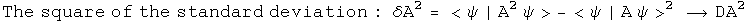
The square of the standard deviation: dA squared = <psi | A squared psi> -<psi| A psi> squared maps to DA squared

One subtlety to note is that a quaternion operator is anti-Hermitian only if the scalar is zero. This is probably the case for classical quantum mechanics, but quantum field theory may require full quaternion operators. The proof of the uncertainty principle shown here is independent of this issue. I do not yet understand the consequence of this point.

To get to the position-momentum uncertainty equation, make these specific maps

A goes to X

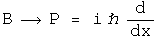
B goes to P = i h bar d by dx

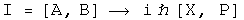
I h bar = the commutator of A, B goes to i h bar the commutator of X, P

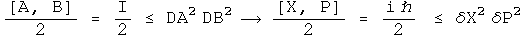
The commutator of A, B over 2 = I over 2 is less than or equal to DA squared DB squared goes to the commutator of X, P over 2 = i h bar over 2 is less than or equal to the standard deviation of X squared times the standard deviation of P squared

The product of the squares of the standard deviation for position and momentum in the x-direction has a lower bound equal to half the expectation value of the commutator of those operators. The proof is in the structure of quaternions.

Implications

There are many interpretations of the uncertainty principle. I come away with two strange observations. First, the uncertainty principle is about quaternions of the form q = Exp[a b I]. With this insight, one can see by inspection that a plane wave Exp[((Et - P.X)/hbar I], or wave packets that are superpositions of plane waves, will have four uncertainty relations, one for the scalar Et and another three for the three-part scalar P.X. This perspective should be easy to generalize.

Second, the uncertainty principle and gravity are related to the same mathematical properties. This proof of the uncertainty relation involved the Schwarz inequality. It is fairly straightforward to convert that inequality to the triangle inequality. Finding geodesics with quaternions involves the triangle inequality. If a complete theory of gravity can be built from these geodesics (it hasn't yet been done :-) then the inequalities may open connections where none appeared before.