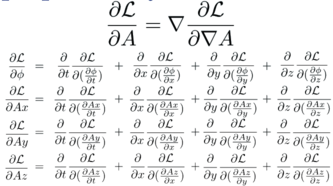
Derive the Euler-Lagrange equations

The Euler-Lagrange equations are used to generate field equations from a Lagrange density. Think of a Lagrange density as every way energy can be traded inside of a box. The action S integrates the Lagrange density (mass per volume) over space and time, resulting in t mass times time.

The action S equals the integral of the Lagrange density over space-time

Notice that the action could be just about any value by integrating over different amounts of time, from a nano-second to a billion years.

The approach is to vary something in the action S so this integral does not change. This means that the "something" is a symmetry of the action. Where there is a symmetry, there is necessarily a conserved quantity.

The variaton of the action S equals 0 equals the integral of the Lagrange density varied with respect to a variable and posibly the derivatives of the variable integrated over space-time

This is a minimization problem, or more formally, the calculus of variations. The first types of minimization problems one learns are about the minimum value of something like a velocity at a point in space-time. This is about a minimization of a function over all of space-time. The mechanics are the same - take a derivative, set it to zero - but the thing that gets plugged in is different.

Examples

  • If the lagrange density is not a function of time, then time is a symmetry and energy is conserved.

  • If the lagrange density is not a function of space, then space is a symmetry and linear momentum is conserved.

  • If the lagrange density is not a function of angle, then rotation is a symmetry and angular momentum is conserved.

Counter example

  • If a lagrange equation is a function of space and time, then energy and momentum are not conserved. This happens for systems that have friction. The energy and momentum go into waste heat. Those terms usually are not included in the Lagrange density.

Deriving the Euler-Lagrange equations

If a Lagrange density depends on a 4-potential a and the derivatives of a, then vary these and find a minimum. This is the heart of the Euler-Lagrange equations.

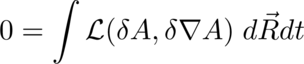
the integral of the lagrange density varied with respect to a and the derivative of a integrated over space-time equals 0

This is a minimum problem with the potential A and its derivative, A'.

1: Start with a Lagrange density that is a function of the potential and its derivatives.

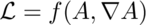
The Lagrange density is a function of the potential and the derivatives of the potential

Note that one is not allowed to vary position or speed. If we were to do the reverse - fix the potential and its derivative, but vary position and velocity - then we would be deriving the force equation from the same Lagrange density.

2: For the action by integrating over a volume of space-time.

The action S equations the integral over space-time of the Lagrange density that is a function of the potential A and the derivatives of the potential A'

3: Vary the action.

Vary the action S which equals the integral over space-time of the partial derivative of the Lagrange density with respect to A while varying A plus the derivative of the Lagrange density with respect to the derivative of A while varying the derivative of A

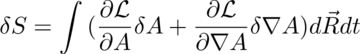
4: The problem is with the variation in A versus the variation is the derivative of A. Use the product rule to get two variations in A.

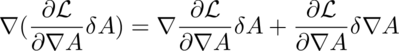
The derivative of the product of the partial derivative of the Lagrange density with respect to Del A times the variation in A equals Del the partial derivative of the Lagrangian with respect to Del A while varying A plus the partial derivative of the Lagrangian with respect to Del A while varying Del A

5: A theorem of Gauss says:

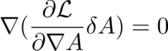
The gradient of the partial derivative of the Lagrangian with respect to Del A while varying A equals zero

so:

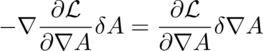
6: Substitute 5 into the variation in 3:

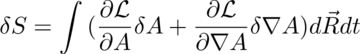
Vary the action S which equals the integral over space-time of the partial derivative of the Lagrange density with respect to A minus the derivative of the Lagrange density with respect to Del A while varying with respect to A

7: The variation will be at the minimum if the variation in the action S is zero, which happens if the integrand is zero:

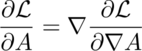
The derivative of the Lagrange density with respect to A is equal to the derivative of the partial derivative of the Lagrange density with respect to Del A

QED

There are so many partial differential equations when using Euler-Lagrange, people with think you are brilliant.