An Introduction to the Standard Model
The Standard Model of physics was developed in the 1970's to explain the ~270 different types of particles seen in colliders (a general introduction is available on wikipedia, and a one page cheat sheet). The part we need to understand is the groups that describe the symmetry of the standard model.
What is a group? A group has an identity, an inverse, and a binary operation (multiplication). One member of the group times another member of the group generates yet another member of the same group. This is a case where the math name is accurate: once in a group, you are always in a group.
The standard model has three continuous groups that characterize three of the four known fundamental forces of nature. The simplest group is known as U(1) and governs electromagnetism via the photon. The reason there is one photon is that the Lie algebra u(1) - note that was a small u! - has one degree of freedom. This group is called the unary group, complex numbers with a norm of 1. The members of this group commute, so it does not matter the order things are written in. Quaternions have this property only when all point in the same or opposite directions, which is the case for when using one quaternion times itself.
The continuous group SU(2) rules the weak force, the stuff driving radioactive decay. Mathematically this is call unitary quaternions, quaternions with a norm of 1. The Lie algebra used to generate this group has three degrees of freedom. That is why the weak force is mediated by three particles, the W+, W-, and the Z.
The group SU(3) is for the strong force whose residual interactions keep nuclei together. Its Lie algebra has eight members, and there are eight gluons.
Animations of Groups
Start with a simple picture, layer pictures together, and we will be able to see what the standard model of particle physics looks like.
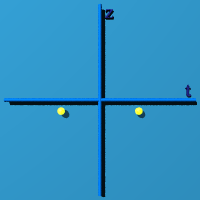
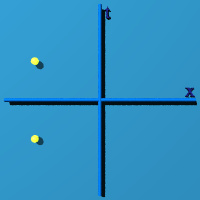
S0 - So simple!
This is the symmetry of +/-R, one number. What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
This is (-1, 0, 0, 0) and (+1, 0, 0, 0). It sits in the center, as quaternions
of the form (n, 0, 0, 0) like to do.
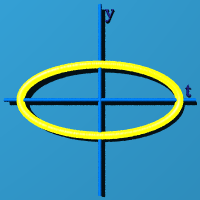
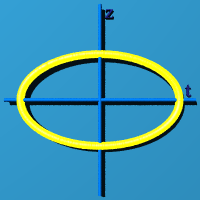
[S1 - The Circle](http://www.theworld.com/%7Esweetser/quaternions/quantum
/standard_model/S1)
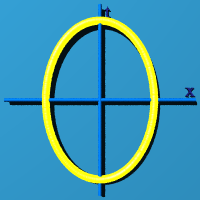
Now we let the sum of squares of 2 numbers equal 1. This creates a circle.
What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
The circle could have any orientation in 3D space. The program choose one at
random.
S2 - Slice of an Expanding/Contracting Sphere
The sum of squares of 3 numbers equal 1. A quaternion has four numbers. One
approach to representing S2 is to set t=0. You get the standard sphere, but
only at the instant of t=0. Blink! What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
That looks like a typical sphere, except it doesn't last long. Three straight
lines appear in the "what was" graph because time is fixed.
Another way to represent S2 is to set x=0. Then you have an edge view of an expanding circle.
What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
Only the "what was left/right" graph has a fixed, straight line graph, because
x=0.
If z=0, at least you can see the "circle-ness"
What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
In the "what was" graphs, it is easy to spot which dimension is set to zero:
it is the straight line.
S3 - A Quaternion Sphere
Now use all 4 terms, and fill in the sphere in both time and space! What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
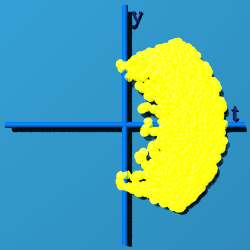
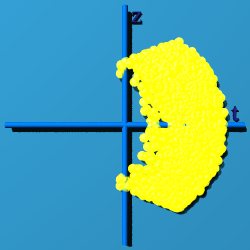
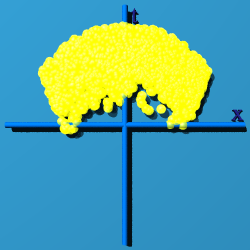
SU(2) - Like S2, the Partial Sphere
The graphs of S2 were all paper thin or fleeting. They do not "fill up"
space-time. The next graph, generated by putting random quaternions into the
expression exp(q-q*), fills up space-time. What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
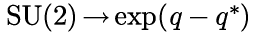
Although more of space-time appears filled, only places were time is greater
than zero have a chance to have an event.
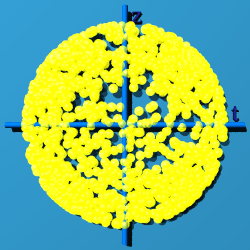
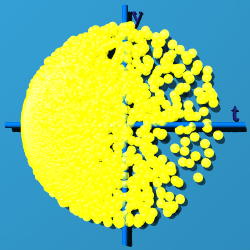
U(1)xSU(2) - Like the Complete Quaternion Sphere S3
SU(2) has only three of the four degrees of freedom available to a quaternion.
There is no way to fill up all of space-time with just SU(2). Now fill
space-time in by multiplying by itself, or q/|q| exp(q-q*) What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
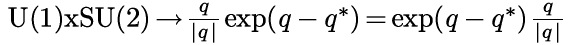
Most of the points cluster on the negative side of the time line.
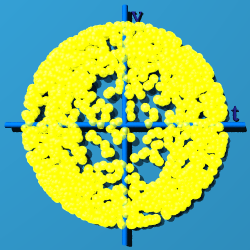
U(1)xSU(2)xSU(3) - The Standard Model
The question is how to generate SU(3)? It has a Lie algebra su(3) that has
eight elements. Based on work done on quaternion quantum mechanics, it is
clear I need to work with the conjugate of one quaternion times another, what
I call the Euclidean product, because q q generates the norm of a quaternion
q, (t2 + x2 + y2 + z2, 0, 0, 0). If we have 2 different quaternions, q and
q', we can write them as q q' as U(1)xSU(2): (q/|q| exp(q-q)) (q'/|q'|
exp(q'-q')). Here is its animation: What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
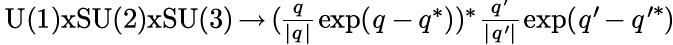
Notice how all of space-time is filled evenly with events. A product of two
quaternions that uses a conjugate different from a standard product because
multiplication is no longer associative ((a b)c does not equal a (b c)). The
norms are preserved, so the norm will remain 1. Eight independent number are
used to make something with a norm of one. The identity is 1, and all elements
have an inverse under what I call "Euclidean multiplication", q q'. Based on
the animation, the group is compact and simply connected. All of this traits
contribute to the conclusion that the symmetry of the standard model can be
represented by quaternions in this way.
It would be great to include gravity, which is all about how measurements change as one moves around a differentiable 4D manifold. Include the metric as part of the calculation of a quaternion product.
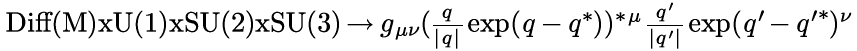
The group Diff(M) is all diffeomorphisms of a compact smooth manifold. It is
at the heart of general relativity. One can imagine this space-time filling
sphere on any compact smooth manifold.
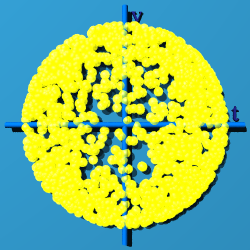
What happens if q=q'? That is shown below:
What was
up/down | What is | What can be
---|---|---
 |
|
 |
|

 |
|
 |
|

What was
near/far | What was
left/right | What can be
that is
The standard model is about the group symmetry of the quaternion
multiplication identity in space-time.
OK, but what does that mean? Here is my take. Observers sit at here-now in space-time, or numerically at (0, 0, 0, 0). An observer sees something out there, and tries to characterize the "thingie". The basic bit of information it can classify is an event. Whatever set of events is collected, they are all tied up in describing this one thingie out there. Every event contributes to the description of the thingie, and so makes a group. The multiplicative identity of a quaternion, (1, 0, 0, 0) is a way to represent the thingie. Almost none of the events map to (1, 0, 0, 0). The events are scattered all around space-time. U(1)xSU(2)xSU(3) is the way to cow-rope all the events and bring them home, while remaining part of the same group, the one thing being observed.