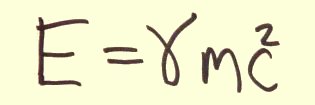
Special relativity using real-valued quaternions only
Early failures
It was obvious in 1910 that quaternions should be perfect to do the job of rotating space and time since quaternions have always been the master of doing rotations in space. This is how a rotation around the x axis is done:
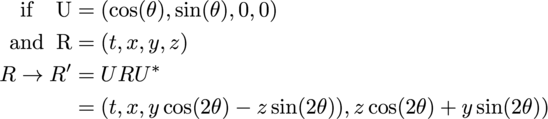
Boosts are rotations involving space and time. There is a well know approach to doing boosts that uses hyperbolic sines and cosines. Just swapping in the hyperbolic functions for their counterparts does not work. So the first people to try this abandoned quaternions and used complex-valued quaternions. The added imaginary factors allowed them to get a boost that was as compact as spatial rotations. They did not worry about loosing the properties of being a division algebra a deal breaker.
The groups for doing spatial rotations versus boosts have a significant technical difference. The group for doing spatial rotations, SO(3), which is compact. The group for doing boosts, SO(1, 3), is not compact. We should not have the expectation that boosts should have the same form as spatial rotations.
An expression that works
I did a hunt for how to represent the Lorentz boost by starting with a hyperbolic rotation, then seeing what was needed to construct the group correctly. About a half hour of hunting and pecking in Mathematica reveled the answer:
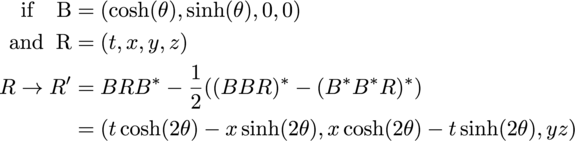
It is fun to compare the boost to the rotation: the former changes the first two terms using hyperbolic functions, while the later operates on the final two terms with the normal trig functions. Some people battle to understand the factor of two on the angles, but I just accept it as is.
There are several places in the physics literature where it is claimed that only complex-valued quaternions can represent the Lorentz group. Sometimes it is good to just play until things work.
Totally-ordered sets in special relativity
Einstein showed in his first paper that the idea of simultaneous depends on the inertial observer. This may lead one to think that all orderings depend on the choice of observer. If we restrict ourselves to straight lines that run through the origin, then [there are some totally-ordered sets|totally_ordered_sets_in_space-time.md]. The subject came up as part of a novel interpretation of quantum mechanics I am calling [Bell's future quantum mechanics|https://bit.ly/BellsFuture]. Click on the links to see more details.