Derive the Maxwell homogeneous equations

The easy way

There are several different roads to the same results, the no monopoles law and Faraday's law, known together as the homogeneous equations. The quickest path is to show how they are vector identities. The divergence of a curl is zero, so if the magnetic field is the curl of the potential A, then there are no magnetic monopoles.

One down, one to go.

Plug the potential definitions of a B and E field into Faraday's law, and watch all the terms drop.

QED.

The path followed here is considerably longer. Everyone uses the Euler-Lagrange equations to derive the source equations, Gauss' law and Ampere's law. For the sake of logical consistency, and to get practice with the details of Euler-Lagrange, the same machinery will be used to derive all four Maxwell equations.

Maxwell defined

The Maxwell equations are the pinnacle of classical physics, the way all light, electric charges, and magnets play with each other gracefully. Here is a one sentence definition:

The Maxwell equations define how a current density is the source of all the
changes in space-time of changes in space-time of a space-time potential
that travels at the speed of light.

The Maxwell equations are a complete set of second order differential equations along with the vector identities. Nothing is missing.¹

The fields defined

A quaternion derivative has a time derivative and three spatial derivatives. A quaternion potential has a scalar potential and three others for space no matter what one's choice of coordinate systems. Construct the complete set of first order changes of a potential by taking the product.

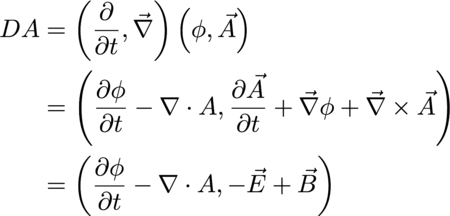
Simple enough.

No, stop. This is amazing enough to repeat.

The most basic complete quaternion derivative of a potential is EM

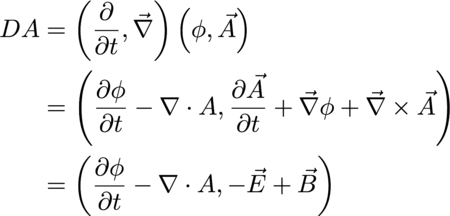
But what about that first term? One of the defining characteristic of light is how its interval is zero. A photon cannot wear a watch. Photons are timeless. The way to implement that quality is to set this gauge term equal to zero like so:

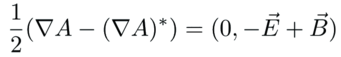
This is a recurring technique. If something travels at the speed of light, there will be non of the four gauge terms:

The electric and magnetic field are unchanged by changing the guage because the gauge terms are always subtracted away.

One enormous subject I have not looked into is what happens if one keeps this gauge term. The resulting physics must describe thing that do not travel at the speed of light. It is the subject of particles with a mass.

The plan

Here is how we will derive the no monopoles law.

• Start with 1 easy term, E~x~
• Pair that with 1 B~x~
• Multiply it out
• Clone lines, filling in E~y~ and E~z~
• Look for patterns

Writing out the Lagrangian

The dot product of the electric and magnetic fields has 24 terms. It is scary, so start simple with one term only, E~x~:

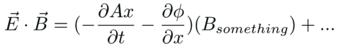
The magnetic field B~x~ has everything not found in E~x~, including both the potentials and derivatives.

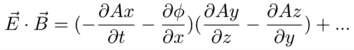
It is seeing details like all four potential terms and all four differentials in each line that makes the Maxwell equations feel so complete.

Multiply this out.

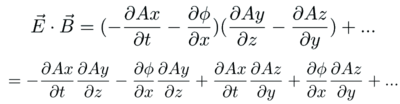
• Half the terms are positive, half are negative, setting up for cancellations.
• Each term has a t, x, y, z-ish part.
• 8 down, 16 to go.

Clone E~x~ to make E~y~ and E~z~ making all necessary substitutions:

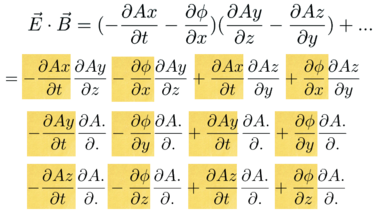
Look for patterns in the partial derivatives:

The electric field terms are in yellow. The top line has the magnetic field, B~x~. None of these has an x, it is pairs of y's and z's.

The next part of the puzzle is to figure out where the rest of the derivative with respect to x go. That will dictate where the other partials go too.

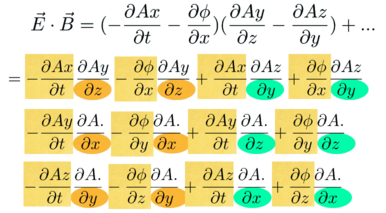
This is the game of curl Sudoku. Fill in the missing values for x, y and z.

All the needed slots are filled in. The Sudoku game is complete.

Now remove some of the details. The dot product of E and B is pretty:

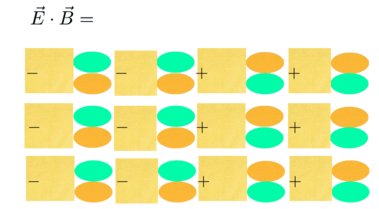
The Lorentz invariant Lagrange density is complete.

Derive the no monopoles law

Plug the 16 terms of the Lagrange density into 20 slots in the Euler-Lagrange equations:

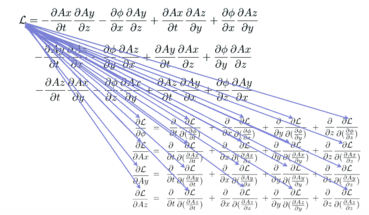
This is a mountain of details. People are much better at spotting patterns.

Do simple things, one at a time. Here is the first Euler-Lagrange equation:

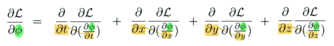
• Only terms with phi matter.
• The derivative repeat.
• That's it.

Here are the terms in the Lagrangian that have a phi:

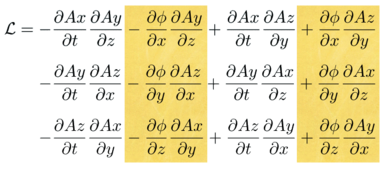
Every term with a phi is mixed. Derivatives of mixed terms is simple:

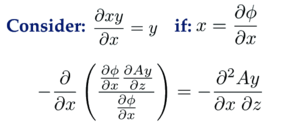
Here's what happens: * After Euler-Lagrange is applied, there is no phi left. * There is 1 term in the numerator, and two partial derivatives. * All three spatial directions appear once. Using these three guides, you should be able to picture how the Lagrange density is changed by applying the Euler-Lagrange equation.

With minuses in one column, and pluses in the other, cancellations happen:

Focus on the example. See how the phi drops, and one has mixed derivatives with opposite signs. Nice.

What is going on in terms of the E and B fields? Look at things row by row:

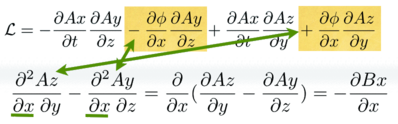
The first line of the Lagrangian has two derivatives of phi with respect to x. After going through the Euler-Lagrange equation, one is left with a second order derivative which is the x derivative of the magnetic field.

Rinse and repeat for y and z:

These cancellations all happen because of a vector identity: the divergence of a curl is zero.

Derive Faraday's law

To continue down this longer road and arrive at Faraday's law, start from the same Lagrangian, but focus on the A~x~ terms:

• The Euler-Lagrange will wipe out the A~x~'s, leading to cancellations.
• The top line is a time derivative of B~x~.
• The second and third lines together form the curl of E~x~.

Here is the pattern:

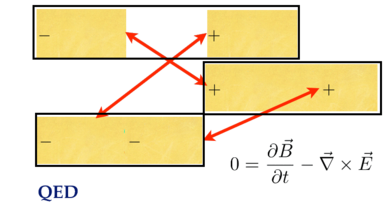
This is Faraday's law.