A Quaternion Algebra Tool Set

Here is a compilation of basic algebra for quaternions. It should look very similar to complex algebra, since it contains three sets of complex numbers, t + x i, t + y j, and t + z k. To strengthen the link, and keep things looking simpler, all quaternions have been written as a pair of a scalar t and a 3-vector V, as in (t, V). All these relations have been tested in a C library and a Java quaternion calculator.

Technical note: it is vital that every tool in this set can be expressed as working with a whole quaternion q. This will make doing quaternion analysis with automorphic functions fruitful.

Parts

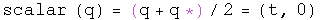
The scalar of q equals q plus its conjugate over two equals \(t, zero\)

The vector of q equals q minus its conjugate over two equals \(zero, V\)

Simple algebra

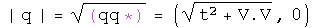
The absolute value of q equals the square root of q times its conjugate equals \(the square root of t squared plus V dot V, 0\)

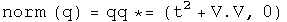
The norm of q equals q times its conjugate equals \(t squared plus V dot V, 0\)

The determinant of q equals q times its conjugate squared equals \(the square of t squared plus V dot V, 0\)

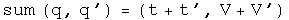
The sum of q and q prime equals \(t plus t', V plus V'\)

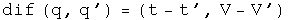
The difference of q and q prime equals \(t minus t', V minus V'\)

The conjugate of q equals q* equals \(t, minus V\)

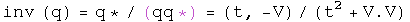
The inverse of q equal q conjugated over its norm equals \(t, -V\) over \(t squared plus V dot V\).

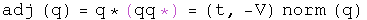
The adjoint of q equals q conjugated times its norm equals \(t, -V\) times \(t squared plus V dot V\).

Multiplication

The Grassman product as defined here uses the same rule Hamilton developed. The Euclidean product takes the conjugate of the first of the two elements (following a tradition from quantum mechanics).

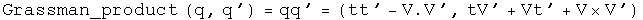
The Grassman product of q and q' equals q times q prime equals \(t t prime minus V dot V prime, t V prime plus V t prime plus V cross V prime\).

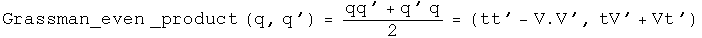
The Grassman even product of q and q' equals q times q prime plus q prime q over two equals \(t t prime minus V dot V prime, t V prime plus V t prime\).

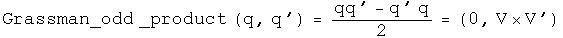
The Grassman odd product of q and q' equals q times q prime minus q prime q over two equals \(zero, V cross V prime\).

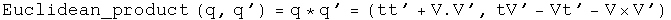
The Euclidean product of q and q' equals q conjugated times q prime equals \(t t prime plus V dot V prime, t V prime minus V t prime minus V cross V prime\).

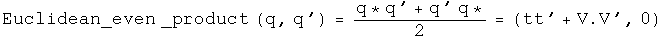
The Euclidean even product of q and q' equals q conjugated times q prime plus q prime q conjugated over two equals \(t t prime plus V dot V prime, zero\).

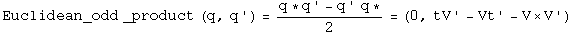
The Euclidean odd product of q and q' equals q conjugated times q prime minus q prime q conjugated over two equals \(zero, t V prime minus V t prime minus V cross V prime\).

Trigonometry

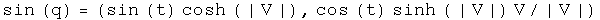
The sine of q equals \(sin t hyperbolic cosine absolute value of V, cosine t hyperbolic sine of the absolute value of V times V normalized to V\)

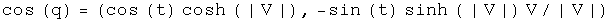
The cosine of q equals \(cos t hyperbolic cosine absolute value of V, minus sine t hyperbolic sine of the absolute value of V times V normalized to V\)

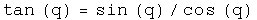
The tangent of q equals the sine of q times the inverse of the cosine of q

Note: since the unit vectors of sine and cosine are the same, these two commute so the order is irrelevant.

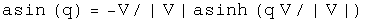
The arcsine of q equals minus V normalized to V times the hyperbolic arcsine of q times V normalized to V.

The arccosine of q equals minus V normalized to V times the hyperbolic arccosine of q.

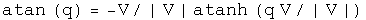
The arctangent of q equals minus V normalized to V times the hyperbolic arctangent of q times V normalized to V.

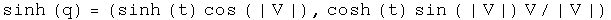
The hyperbolic sine of q equals \(hyperbolic sin t cosine absolute value of V, hyperbolic cosine t sine of the absolute value of V times V normalized to V\)

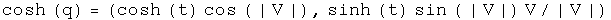
The hyperbolic cosine of q equals \(hyperbolic cos t cosine absolute value of V, hyperbolic sine t sine of the absolute value of V times V normalized to V\)

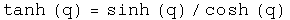
The hyperbolic tangent of q equals the hyperbolic sine of q times the inverse of the hyperbolic cosine of q

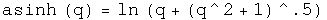
The hyperbolic arcsine of q equals the natural log of \(q plus the square root of q squared plus q\).

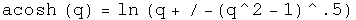
The hyperbolic arccosine of q equals the natural log of \(q plus or minus the square root of q squared minus one\).

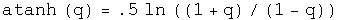
The hyperbolic arctangent of q equals one half times the natural log of \(one plus q over one minus q\).

Powers

The exponential of q equals \(e to the t cosine absolute value of V, e to the t sine of the absolute value of V times V normalized to V\)

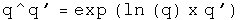
q raised to the q prime equals the exponential of the natural log of q time q prime.

Logs

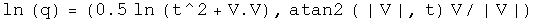
The natural log of q equals (one half times the natural log of t squared plus V dot V, the arctan of absolute value of V, angle t time V normalized to V.

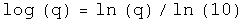
The log base 10 equals the natural log of q over the natural log of 10.

Quaternion exponential multiplication

The Grassman product of two exponentials q and q' equals the even Grassman product times the absolute value of the odd Grassman product times the exponential of pi over 2 times the odd Grassman product normalized to itself.

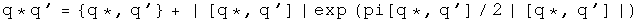
The Euclidean product of two exponentials q and q' equals the even Euclidean product times the absolute value of the odd Euclidean product times the exponential of pi over 2 times the odd Euclidean product normalized to itself.

Andrew Millard suggested the result for the Grassman product.